Graph Neural Networks (GNNs) are a type of neural network designed to directly operate on graphs, a data structure consisting of nodes (vertices) and edges connecting them. GNNs have revolutionized how we analyze and utilize data structured in the form of a graph. Whenever you hear about groundbreaking discoveries in fields like drug development, social media analysis, or fraud detection, there’s a good chance that GNNs are playing a part behind the scenes.
In this article, we’ll start with a gentle introduction to Graph Neural Networks and follow with a comprehensive technical deep dive.
About us: Viso Suite is the end-to-end computer vision platform. With Viso Suite, it becomes possible for enterprises to start using machine learning without a single line of code. Book a demo with us to learn more.
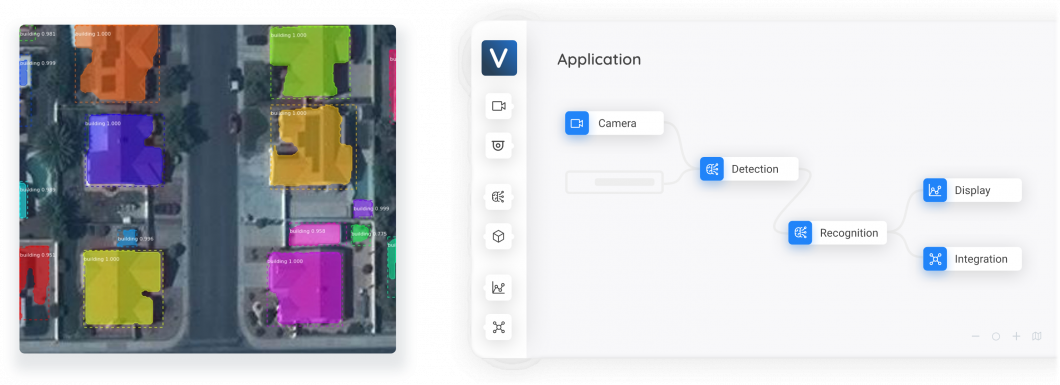
Prediction Tasks Performed by GNNs
The primary goal of GNNs is to learn a representation (embedding) of the graph structure. The GNN captures both the properties of the nodes (what the node contains) and the topology of the graph (how these nodes connect).
These representations are useful for various tasks such as node classification (determining the label of a node), link prediction (predicting the existence of an edge between two nodes), and graph classification (classifying entire graphs).
For example, social network apps (Facebook) extensively use GNNs. Here the GNNs can predict user behavior not just based on their profile, but also their friends’ activities and social circles. Here is what the GNN does:
- Node-level prediction: Predicting the category of a node (e.g. Does this person eat a burger (predicting based on the kind of friends the person has, or activities the person does).
- Edge-level prediction: Predicting the likelihood of a connection between two nodes (e.g., suggesting new friends in a social network or what next Netflix video to play).
- Graph level prediction: Classifying the entire graph based on its structure and node properties (e.g., deciding whether a new molecule is a suitable drug, or predicting what would be the aroma of the new molecule).
Understanding the Basics of Graphs
To understand the Graph Neural Network (GNN), we need to learn its most basic element, which is a Graph. A graph data structure represents and organizes not just the data points but also emphasizes the relationships between data points.
Vertices and Edges
A graph is a collection of points (nodes) connected by lines (edges). Vertices represent entities, objects, or concepts, while edges represent relationships or connections between them.
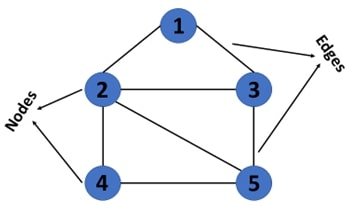
In the context of the social network, the nodes can be a person, and the edges can be the kind of relationship (the person follows, etc.)
Directed vs Undirected Graphs
In a directed graph, edges have a direction, indicating the flow of the relationship. The direction can be who follows whom (you might be following person A, but person A doesn’t follow you back), in the context of a social network.
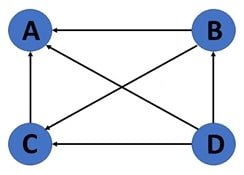
In an undirected graph, edges do not have a direction, simply indicating a connection between two vertices. E.g. on Facebook, if you accept a friend request, then you can see their posts, and they can see back yours. The relationship is mutual here.
Weighted Graph
The edges have a weight associated with them.
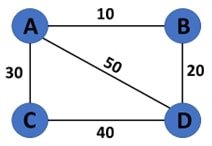
What is Graph Representation?
Graph representation is a way to encode graph structure and features for processing by neural networks. Graphs embed the node’s data and also the relationship between the data points. To represent these connections between the nodes, graph representation is required.
Here are some of the most used graph representations for Deep Learning.
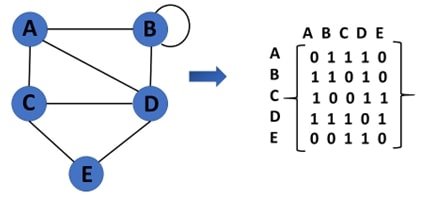
Adjacency Matrix
This is a matrix listing all the vertices connected to that vertex (all the nodes connected to a node). E.g. here, node A has nodes B and C connected to it, there in the array, the corresponding value is 1. When a connection doesn’t exist, it has 0 in the array.
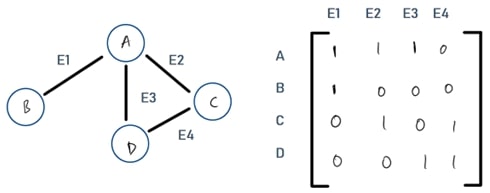
Incidence Matrix
A matrix of size NxM where N is the number of nodes and M are edges of the graph. In simple terms, it is used to represent the graph in matrix form. The value is 1 if the node has a particular edge, and 0 if it does not. E.g., A has edge E1 connected to it, therefore in the incidence matrix, it is a 1. Whereas node A doesn’t have edge E4 connected to it, therefore it is denoted by 0 in the matrix.
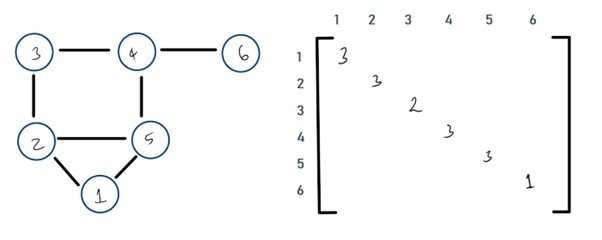
Degree Matrix
A diagonal matrix which contains the number of edges attached to each node.
Unique Characteristics of Graph Data
Graph data structure models real-world data efficiently due to its special characteristics. This is what makes them different from matrices used in Convolutional Neural Networks (CNNs).
To be able to work on graph data structure, GNNs were developed. Before diving into GNNs let’s see what those unique characteristics of graphs are:
- Connections: Unlike tabular data where entities exist in isolation, graph data revolves around connections between entities (nodes). These connections joining the nodes, represented by edges, hold crucial information that makes the data valuable and is central to understanding the system.
- No Structure: Traditional data resides in ordered grids or tables. Graphs, however, have no inherent order, and their structure is dynamic (the nodes are spread out randomly and change their positions). Which is what makes it useful for modeling dynamic real-world data.
- Heterogeneity: In a graph, points (nodes) and connections (edges) can stand for different things like people, proteins, or transactions, each having its characteristics.
- Scalability: Graphs can become very large, including complex networks with millions of connections and points, which makes them difficult to store and analyze.
Graph Neural Networks vs Neural Networks
To better understand Graph Neural Networks (GNNs), it’s essential to first know how they differ from traditional Neural Networks (NNs). Starting with NNs as a foundation, we can then explore how GNNs build on this to handle graph-structured data, making the concept clearer and more approachable.
Here are some of the differences between NNs and GNNs.
Data Structure
- Neural Networks (NNs): Traditional neural networks, including their variants like Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNNs), are primarily designed for grid-like data structures. This includes images (2D grids of pixels) for CNNs and sequential data (time series or text) for RNNs.
- Graph Neural Networks (GNNs): GNNs are specifically designed to handle graph data. Graphs not only store data points but also the complex relationships and interconnections between data points.
Data Representation
- NNs: Data input into traditional neural networks needs to be structured, such as vectors for fully connected layers, multi-dimensional arrays for CNNs (e.g., images), or sequences for RNNs.
- GNNs: Input data for GNNs is in the form of graphs, where each node can have its features (attribute vectors), and edges can also have features representing the relationship between nodes.
Operation
- NNs: Operations in neural networks involve matrix multiplications, convolution operations, and element-wise operations, applied in a structured manner across layers.
- GNNs: GNNs operate by aggregating features from a node’s neighbors through a process called message passing. This involves aggregating the current node’s features with the neighbor node’s features (read more on this operation below).
Learning Task
- NNs: Traditional neural networks are well-suited for tasks like image classification, object detection (CNNs), and sequence prediction or language modeling (RNNs).
- GNNs: GNNs excel at tasks that require understanding the relationships and interdependencies between data points, such as node classification, link prediction, and graph classification.
Interpretability
The ability to understand the inner workings and how models make their decisions or predictions.
- Neural Networks (NNs): While NNs can learn complex patterns in data, interpreting these patterns and how they relate to the structure of the data can be challenging.
- Graph Neural Networks (GNNs): GNNs, by operating directly on graphs, offer insights into how relationships and structure in the data contribute to the learning task. This is extremely valuable in domains such as drug discovery or social network analysis.
Types of GNNS
Graph Neural Networks (GNNs) have evolved into various architectures to address different challenges and applications. Here are a few of them.
Graph Convolutional Network (GCN)
The most popular and also a foundational type of GNN. The key idea behind GCNs is to update the representation of a node by aggregating and transforming the features of its neighboring nodes and itself (inspired by CNNs). This aggregation mechanism enables GCNs to capture the local graph structure around each node. GCNs are widely used for node classification, graph classification, and other tasks where understanding the local structure is crucial.
Deep Graph Convolutional Neural Network II (DGCNNII)
This architecture uses a deep graph convolutional neural network architecture for graph classification. It is improved upon GCN. This new architecture is based on a non-local message-passing framework and a spatial graph convolution layer. It is shown to outperform many other graph neural network methods on graph classification tasks.
Graph Attention Networks (GATs)
Introduce attention mechanisms to the aggregation step in GNNs (adding weight to the aggregation step).
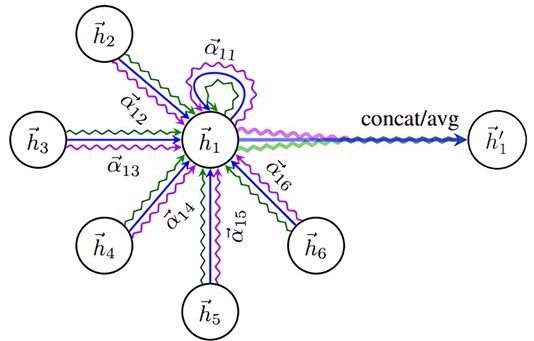
In GATs, the importance of each neighbor’s features is dynamically weighted (the different colors of arrows in the image) during the aggregation process, allowing the model to focus more on relevant neighbors for each node. This approach is beneficial in graphs where not all connections are equally important or some nodes overpower the rest of the nodes (e.g. an influence with millions of followers), and it can lead to more expressive node representations. GATs are particularly useful for tasks that benefit from distinguishing the significance of different edges, such as in recommendation systems or social network analysis.
Graph Recurrent Networks (GRNs)
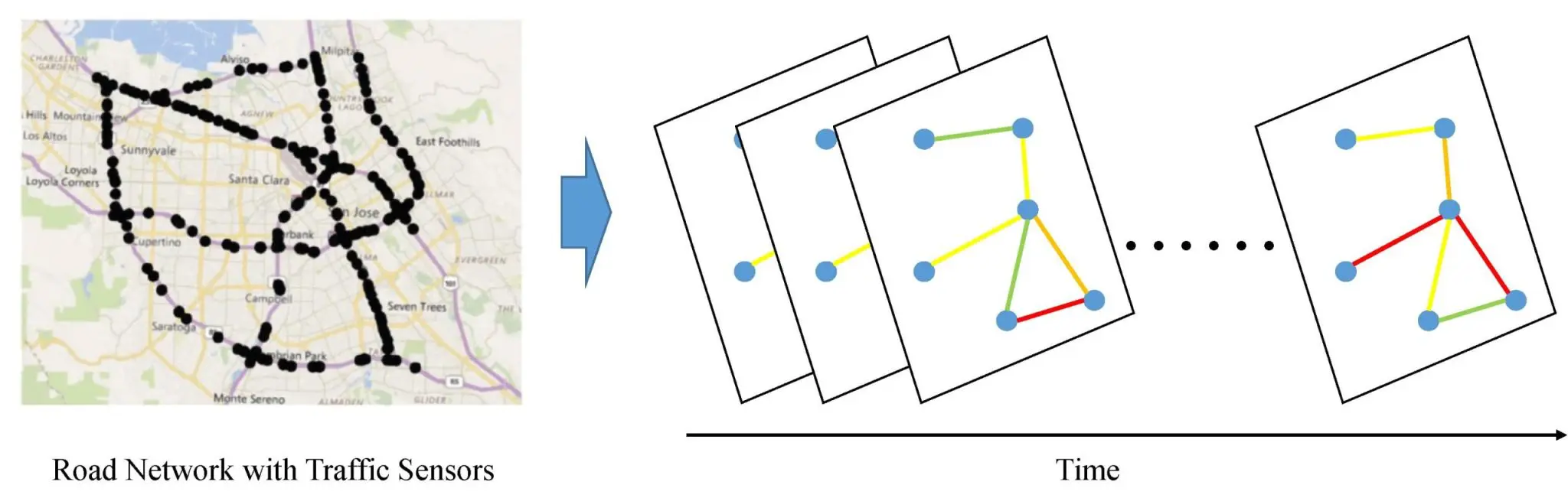
Combine the principles of recurrent neural networks (RNNs) with graph neural networks. In GRNs, node features are updated through recurrent mechanisms, allowing the model to capture dynamic changes in graph-structured data over time. Examples of applications include traffic prediction in road networks and analyzing time-evolving social networks.
Graph Autoencoders (GAEs)
Designed for unsupervised learning tasks on graphs. A GAE learns to encode the graph (or subgraphs/nodes) into a lower-dimensional space (embedding) and then reconstructs the graph structure from these embeddings. The objective is to learn representations that capture the essential structural and feature information of the graph. GAEs are particularly useful for tasks such as link prediction, clustering, and anomaly detection in graphs, where explicit labels are not available.

Graph Generative Networks
Aim to generate new graph structures or augment existing ones. These models learn the distribution of observed graph data and can generate new graphs that resemble the training data. This capability is valuable for drug discovery, where generating novel molecular structures is of interest. Also in social network analysis, where simulating realistic network structures can help understand network dynamics.
How Do GNNs Work
GNNs work by leveraging the structure of graph data, which consists of nodes (vertices) and edges (connections between nodes), to learn representations for nodes, edges, or entire graphs. They combine these features into a new feature matrix (the current nodes and the neighboring nodes).
This new feature matrix is updated in the current node. When this process is done multiple times, with all the nodes in the graph, as a result, each node learns something about every other node.
GNN Learning Steps
- Message Passing: In each layer, information is passed between nodes in the graph. A node’s current state is updated based on the information from its neighbors. This is done by aggregating the information from the neighbors and then combining it with the node’s current state. This is also called graph convolution (inspired by CNNs). In CNNs, the information from the neighbor pixels is integrated into the central pixel, similarly in GNNs, the central node is updated with aggregated information about its neighbors.
- Aggregate: There are different ways to aggregate the information from a node’s neighbors. Some common methods include averaging, taking the maximum, or using a more complex function like a recurrent neural network.
- Update: After the information from the neighbors has been aggregated, it is combined with the node’s current state, forming a new state. This new node state contains information about the neighboring nodes. Aggregate and update are the most important steps in GNNs. Here is the formal definition:

- Output: The final node, edge, or graph representations is useful for tasks like classification, regression, or link prediction.
- Multiple Layers: The message-passing process can be repeated for multiple layers. This allows nodes to learn information about their neighbors’ neighbors, and so on. The number of layers formally called hops is a hyperparameter.
What is a Hop?
In GNNs, a hop refers to the number of steps a message can travel from one node to another. For example, here the GNN has 2 layers, and each node incorporates information from its direct neighbors and its neighbors’ neighbors.
However, one needs to be careful at choosing the number of layers or hops, as too many layers can lead to all the nodes having roughly the same values (over-smoothing).
What is Oversmoothing?
Oversmoothing is a challenge that arises when too many layers of message passing and aggregation are used in a GNN.
As the depth of the network increases, the representations of nodes across different parts of the graph may become indistinguishable. In extreme cases, all node features converge to a similar state, losing their distinctive information.
This happens because, after many iterations of smoothing, the node features have aggregated so much information from their neighborhoods that the unique characteristics of individual nodes are washed out.
Smoothing in GNNs
Smoothing in GNNs refers to the process through which node features become more similar to each other. This results from the repeated application of message passing and aggregation steps across the layers of the network.
As this process is applied through multiple layers, information from a node’s wider and wider neighborhood is integrated into its representation.
Addressing Oversmoothing
- Skip Connections (Residual Connections): Similar to their use in CNNs, skip connections in GNNs can help preserve initial node features by bypassing some layers, effectively allowing the model to learn from both local and global graph structures without over-smoothing.
- Attention Mechanisms: By weighting the importance of neighbors’ features dynamically, attention mechanisms can prevent the uniform blending of features that leads to over-smoothing.
- Depth Control: Carefully design the network depth according to the graph’s structural properties.
- Normalization Techniques: Techniques like Batch Normalization or Layer Normalization can help maintain the distribution of features across GNN layers.
Applications of GNNs
GNNs have lived to their theoretical potential and are now actively impacting various real-world domains. So, how powerful are graph neural networks? Here’s a glimpse of its applications:
Social Networks
- Community Detection: Identifying communities of users based on their interactions, interests, or affiliations. This is useful for targeted advertising, content recommendation, or anomaly detection.
- Link Prediction: Predicting new connections between users based on existing relationships and network structure. This can be valuable for friend recommendations or identifying potential influencers.
- Sentiment Analysis: Analyzing the sentiment of user posts or conversations by considering the context and relationships within the network. This can help understand public opinion or brand perception.
Recommendation Systems
- Collaborative Filtering with GNNs: Going beyond traditional user-item interactions, GNNs leverage user relationships to personalize recommendations by incorporating social influence and content similarity among users.
- Modeling User-Item Interactions: Capturing the dynamic nature of user preferences by considering the evolution of user relationships and item popularity within a network.
- Explainable Recommendations: By analyzing how information propagates through the network, GNNs can offer insights into why certain items are recommended, increasing transparency and trust in the system.
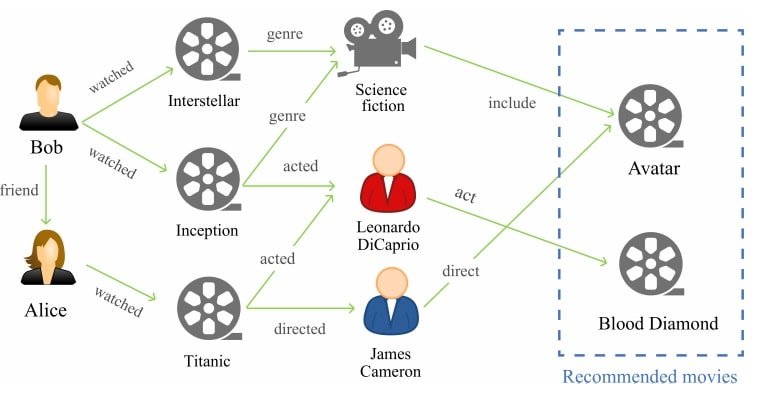
Bioinformatics
- Protein-Protein Interaction Networks: Predicting protein-protein interactions based on their structural and functional similarities, aiding in drug discovery and understanding disease mechanisms.
- Gene Regulatory Networks: Analyzing gene expression data and network structure to identify genes involved in specific biological processes or disease development.
- Drug Discovery: Leveraging GNNs to predict the efficacy of drug candidates by considering their interactions with target proteins and pathways within a network.

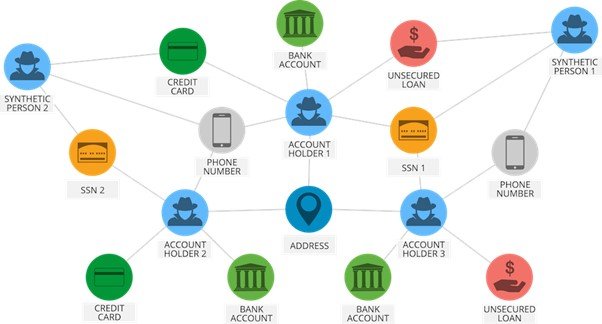
Fraud Detection
Graphs can represent financial networks, where nodes might be entities (such as individuals, companies, or banks), and edges could represent financial transactions or lending relationships. This is useful for fraud detection, risk management, and market analysis.
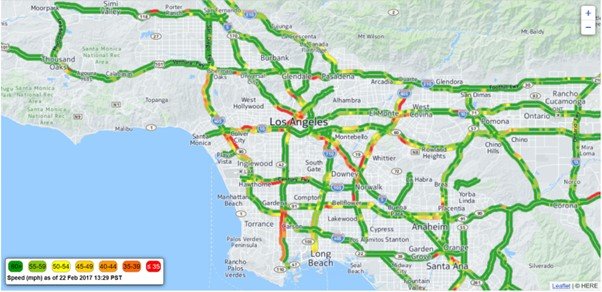
Traffic Flow Prediction
Predicting traffic congestion and optimizing traffic light timings for smart cities by modeling the road network and vehicle flow dynamics.
Cybersecurity
Detecting malicious activities and identifying vulnerabilities in computer networks by analyzing network traffic and attack patterns.
Challenges of GNNs
Despite the impressive progress and potential of GNNs, several research and implementation challenges and limitations remain. Here are some key areas.
Scalability
Many GNN models struggle to efficiently process large graphs due to the computational and memory requirements of aggregating features from a node’s neighbors. This becomes particularly challenging for graphs with millions of nodes and edges, common in real-world applications like social networks or large knowledge graphs.
Oversmoothing
A note on over-smoothing for graph neural networks, as previously mentioned, the depth of a GNN increases, and the features of nodes in different parts of the graph can become indistinguishable. This over-smoothing problem makes it difficult for the model to preserve local graph structures, leading to a loss of performance in node classification and other tasks.
Dynamic graphs
Many real-world graphs are dynamic, with nodes and edges being added or removed over time. Most GNN architectures are designed for static graphs and struggle to model these temporal dynamics effectively.
Heterogeneous graphs
Graphs often contain different types of nodes and edges (heterogeneous graphs), each with its features and patterns of interaction. Designing GNN architectures that can effectively learn from heterogeneous graph data is a challenging task. This requires capturing the complex relationships between different types of entities.
Generalization Across Graphs
Many GNN models are trained and tested on the same graph or graphs with similar structures. However, models often struggle to generalize to entirely new graphs with different structures, limiting their applicability.
Future Work in Graph Neural Networks (GNNs)
Interpretability and Explainability
Making GNN models more understandable is a key area because it is crucial for sectors like healthcare, and finance. Only by understanding how the models make predictions can create trust and facilitate their adoption.
Dynamic and Temporal Graph Modeling
Enhancing the ability of GNNs to model and predict changes in dynamic graphs over time is a key area of research. This includes not only capturing the evolution of graph structures but also predicting future states of the graph.
Heterogeneous Graph Learning
Advancing techniques for learning from heterogeneous graphs, which contain multiple types of nodes and relationships is a key area of ongoing research. This involves creating models that can effectively leverage the rich semantic information in these complex networks.



